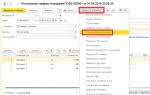
Рассмотрим две основные концепции решения актуальной проблемы определения нормы дисконта — и .
Концепция альтернативной доходности
В рамках безрисковая норма дисконта определяется либо на уровне депозитных ставок банков высшей категории надежности, либо приравнивается к ставке рефинансирования Центрального банка России (такой подход предложен в методических рекомендациях, разработанных в Сбербанке РФ). Норму дисконта можно определить и по формуле И. Фишера.
В Методических рекомендациях указаны различные виды нормы дисконта . Коммерческую норму , как правило, определяют с учетом концепции альтернативной доходности . Свою собственную норму дисконта оценивают участники проекта самостоятельно. Правда, в принципе возможен и согласованный подход, когда все участники проекта ориентируются на коммерческую норму дисконта.
Для проектов, имеющих высокую социальную значимость, определяют социальную норму дисконта . Она характеризует минимальные требования к так называемой общественной эффективности реализации инвестиционного проекта. Обычно устанавливается она централизованно.
Исчисляют также бюджетную норму дисконта , отражающую альтернативную стоимость использования бюджетных средств и устанавливаемую исполнительными органами власти федерального, субфедерального или муниципального уровня.
В каждом конкретном случае уровень принятия решения зависит от того, за счет средств какого бюджета финансируется данный инвестиционный проект.
Концепция средневзвешенной стоимости капитала
Является показателем, характеризующим стоимость капитала так же, как ставка банковского процента характеризует стоимость привлечения кредита.
Отличие средневзвешенной стоимости капитала от банковской ставки заключается в том, что этот показатель не подразумевает равномерных выплат, вместо этого требуется, чтобы суммарный приведенный доход инвестора был таким же, какой обеспечила бы равномерная выплата процентов по ставке, равной средневзвешенной стоимости капитала.
Средневзвешенная стоимость капитала широко используется в инвестиционном анализе, его значение используется для дисконтирования ожидаемых доходов от инвестиций, расчета окупаемости проектов, в оценке бизнеса и других приложениях.
Дисконтирование будущих денежных потоков со ставкой, равной средневзвешенной стоимости капитала , характеризует обесценивание будущих доходов с точки зрения конкретного инвестора и с учетом его требований к доходности инвестированного капитала.
Таким образом, концепция альтернативной доходности и концепция средневзвешенной стоимости капитала предполагают различные подходы к определению нормы дисконта.
Проводим классический фундаментальный анализ сами. Определяем справедливую цену по формуле. Принимаем инвестиционное решение. Особенности фундаментального анализа долговых активов, облигаций, векселей. (10+)
Классический (фундаментальный) анализ
Универсальная формула справедливой цены
Классический (фундаментальный) анализ основан на положении, что у объекта инвестирования есть справедливая цена. Эта цена может быть вычислена по формуле:
Si - сумма дохода, который будет получен от инвестирования в i-ом году, считая от текущего в будущее, ui - альтернативная доходность вложений за этот период (с текущего момента до выплаты i-й суммы).
Например, Вы приобретаете облигацию с погашением через 3 года с выплатой единовременно всей суммы основного долга и процентов по ней. Сумма выплаты по облигации вместе с процентами составит 1500 рублей. Альтернативную доходность вложений определим, например, по доходности депозита в Сбербанке. Пусть будет 6% годовых. Альтернативная доходность составит 106% * 106% * 106% = 119%. Справедливая цена получается равной 1260.5 рублей.
Приведенная формула не очень удобна, так как альтернативная доходность обычно предполагается по годам (даже в примере мы брали годовую доходность и возводили в третью степень). Преобразуем ее к годовой альтернативной доходности

здесь vj - альтернативная доходность вложений за j-й год.
Почему все активы не стоят свою справедливую цену?
Несмотря на свою простоту, приведенная формула не позволяет точно определить стоимость объекта инвестирования, так как содержит показатели, которые нужно прогнозировать для будущих периодов. Альтернативная доходность вложений в будущем нам неизвестна. Мы можем только предполагать, какие ставки будут на рынке в тот момент. Особенно большие погрешности это вносит для инструментов с большими сроками погашения или без таковых (акции, консоли). С суммой платежей тоже не все однозначно. Даже для долговых ценных бумаг (облигаций с фиксированной доходностью, векселей и т. д.), для которых, вроде бы, суммы платежей определены условиями выпуска, реальные платежи могут отличаться от планируемых (а в формуле стоят суммы именно реальных, а не планируемых платежей). Это происходит при дефолте или реструктуризации долга, когда эмитент не может выплатить всю обещанную сумму. Для долевых ценных бумаг (акций, долей, паев и т. д.) суммы этих платежей вообще зависят от результатов деятельности компании в будущем, и соответственно, от общей экономической конъюнктуры в те периоды.
Таким образом, точно рассчитать по формуле справедливую цену невозможно. Формула дает лишь качественное представление о факторах, влияющих на справедливую цену. На основе этой формулы можно выработать формулы для ориентировочной оценки цены актива.
Оценка справедливой цены долгового актива (с фиксированными платежами), облигации, векселя

В новой формуле Pi - сумма, обещанная к выплате в соответствующий период, ri - дисконт, основанный на нашей оценке надежности вложений. В нашем предыдущем примере пусть надежность вложений в Сбербанк мы оцениваем как 100%, а надежность нашего заемщика - как 90%. Тогда оценка справедливой цены составит 1134.45 рублей.
К сожалению в статьях периодически встречаются ошибки, они исправляются, статьи дополняются, развиваются, готовятся новые. Подпишитесь, на новости , чтобы быть в курсе.
Если что-то непонятно, обязательно спросите!
Задать вопрос. Обсуждение статьи.
Еще статьи
Когда менять машину на новую? Обслуживать ли автомобиль у дилера? Плат...
Когда имеет смысл обновить машину? Точный математический ответ. Стоит ли проводи...
Паевые инвестиционные фонды, ПИФ, паи. Типы, виды, категории, классифи...
Особенности паевых инвестиционных фондов разных видов. Инвестиционная привлекате...
Спекуляции, инвестиции, в чем разница...
Как отличить спекуляции от инвестиций? Выбираем инвестиции....
Отраслевые, индексные фонды, массовые инвесторы, спекулянты - техничес...
Особенности отраслевых инвесторов, фондов, массового инвестора, спекулянтов - те...
Кредиты на неотложные нужды, траты. Кредитные карты. Правильно выбирае...
Подбираем и пользуемся правильной хорошей кредитной картой. Бережем Кредитную ис...
Выбираем банк для вклада, депозита осмысленно. Обратим внимание. Госуд...
Не каждый банк подойдет для вложений в депозиты. Государственная гарантия защища...
Квалифицированный инвестор. Статус. Признание. Требования. Критерии...
Квалифицированный инвестор - концепция, смысл. Получение статуса, признание...
Инвестируем в понятные простые проекты. Анализируем объекты вложений. ...
Хорошие инвестиции в понятные и простые проекты. Минимум посредников. Наличие пл...
Доходность. Наиболее существенным параметром, знание которого необходимо при анализе операций с фондовыми ценностями, является доходность. Она вычисляется по формуле
d = ,
(1)
где d -
доходность операций, %;
D - доход, полученный владельцем финансового инструмента;
Z - затраты на его приобретение;
- коэффициент, пересчитывающий доходность на заданный интервал времени.
Коэффициент имеет вид
= Т /t (2)
где Т - интервал времени, на который пересчитывается доходность;
t - интервал времени, за который был получен доход D.
Таким образом, если инвестор получил доход, допустим, за 9 дней (t = 9), то при вычислении доходности за финансовый год (Т = 360) численное значение коэффициента т будет равно:
= 360: 9 = 40
Необходимо отметить, что обычно доходность операций с финансовыми инструментами определяется в расчете на один финансовый год, в котором 360 дней. Однако при рассмотрении операций с государственными ценными бумагами (в соответствии с письмом ЦБ РФ от 05.09.95 № 28-7-3/А-693) Т принимается равным 365 дням.
В качестве иллюстрации расчета доходности финансового инструмента рассмотрим следующий модельный случай. Осуществив операцию купли-продажи с финансовым инструментом, брокер получил за 9 дней доход, равный D =
1 000 000 руб., причем рыночная стоимость энного финансового инструмента Z
= 10 000 000 руб. Доходность данной операции в пересчете на год:
d =
=  =
=  = 400%.
= 400%.
Доход. Следующим важным показателем, используемым при расчете эффективности операций с ценными бумагами, является доход, полученный при этих операциях. Он вычисляется по формуле
D = d + , (3)
где d - дисконтная часть дохода;
- процентная часть дохода.
Дисконтный доход. Формула для расчета дисконтного дохода имеет вид
d = (Р пр -Р пок), (4)
где Р пр - цена продажи финансового инструмента, с которым осуществляются операции;
Р пок - цена приобретения финансового инструмента (отметим, что в выражении для доходности Р пок = Z).
Процентный доход. Процентный доход определяется как доход, полученный от процентных начислений по данному финансовому инструменту. При этом необходимо рассмотреть два случая. Первый, когда процентный доход начисляется по простой процентной ставке, и второй, когда процентный доход начисляется по сложной процентной ставке.
Схема начисления дохода по простой процентной ставке. Первый случай характерен при начислении дивидендов по привилегированным акциям, процентов по облигациям и простых процентов по банковским вкладам. В этом случае инвестиции в размере Х 0 руб. через промежуток времени, равный п процентным выплатам, приведут к тому, что инвестор будет обладать суммой, равной
Х n -Х 0 (1 + n ). (5)
Таким образом, процентный доход в случае схемы простого начисления процентов будет равен:
= X n - Х 0 = Х 0 (1 + n ) - Х 0 = Х 0 n, (6)
где Х n - сумма, образующаяся у инвестора через п процентных выплат;
Х 0 - первоначальные инвестиции в рассматриваемый финансовый инструмент;
- величина процентной ставки;
п - число процентных выплат.
Схема начисления дохода по сложной процентной ставке. Второй случай характерен при начислении процентов по банковским вкладам по схеме сложного процента. Такая схема выплат предполагает начисление процентов как на основную сумму, так и на предыдущие процентные выплаты.
Инвестиции в размере Х 0 руб. после первой процентной выплаты дадут сумму, равную
X 1 -X 0 (1 + ).
При второй процентной выплате проценты будут начисляться на сумму X 1 . Таким образом, после второй процентной выплаты инвестор будет обладать суммой, равной
Х 2 – X 1 (1 + ) - Х 0 (1 + )(1 + ) = Х 0 (1 + ) 2 .
Следовательно, после n -й процентной выплаты у инвестора будет сумма, равная
Х n = Х 0 (1 +) n . (7)
Поэтому процентный доход в случае начисления процентов по схеме сложного процента будет равен
= Х n -Х 0 = Х 0 (1+ ) n – Х 0 . (8)
Доход с учетом налогообложения. Формула для вычисления дохода, получаемого юридическим лицом при совершении операций с корпоративными ценными бумагами, имеет вид
D = d (1- д) + (1- п), (9)
где д - ставка налога на дисконтную часть дохода;
п - ставка налога на процентную часть дохода.
Дисконтный доход юридических лиц (d) подлежит налогообложению в общем порядке. Налог взимается у источника доходов. Процентный доход () облагается у источника этих доходов.
Основные типы задач, встречающихся при осуществлении операций на фондовом рынке
Задачи, которые чаще всего встречаются при анализе параметров операций на фондовом рынке, требуют ответа, как правило, на следующие вопросы:
Какова доходность финансового инструмента или доходность какого финансового инструмента выше?
Чему равен рыночная стоимость ценных бумаг?
Чему равен суммарный доход, который приносит ценная бумага (процентный или дисконтный)?
Каков срок обращения ценных бумаг, которые выпускаются с заданным дисконтом, для получения приемлемой доходности? и т.п.
Однако основная масса других, значительно более сложных задач при всем многообразии их формулировок, как это ни удивительно, имеет общий подход к решению. Он состоит в том, что при нормально функционирующем фондовом рынке доходность различных финансовых инструментов приблизительно равна. Этот принцип можно записать следующим образом:
d 1 d 2 . (10)
Используя принцип равенства доходностей, можно составить уравнение для решения поставленной задачи, раскрывая формулы для доходности (1) и сокращая сомножители. При этом уравнение (10) приобретает вид
 =
=  (11)
(11)
В более общем виде, используя выражения (2)-(4), (9), формулу (11) можно преобразовать в уравнение:

 . (12)
. (12)
Преобразуя данное выражение в уравнение для вычисления искомого в задаче неизвестного, можно получить окончательный результат.
Алгоритмы решения задач
Задачи на вычисление доходности. Методика решения подобных задач выглядит следующим образом:1) определяется тип финансового инструмента, для которого требуется вычислить доходность. Как правило, тип финансового инструмента, с которым совершаются операции, известен заранее. Эта информация необходима для определения характера дохода, которого следует ожидать от этой ценной бумаги (дисконтный или процентный), и характера налогообложения полученных доходов (ставка и наличие льгот);
2) выясняются те переменные в формуле (1), которые необходимо найти;
3) если в результате получилось выражение, позволяющее составить уравнение и решить его относительно искомого неизвестного, то на этом процедура решения задачи практически заканчивается;
4) если не удалось составить уравнение относительно искомого неизвестного, то формулу (1), последовательно используя выражения (2)-(4), (6), (8), (9), приводят к такому виду, который позволяет вычислить неизвестную величину.
Приведенный выше алгоритм можно представить схемой (рис. 10.1).
Задачи на сравнение доходности. При решении задач данного типа в качестве исходной используется формула (11). Методика решения задач подобного типа выглядит следующим образом:

Рис. 10.1. Алгоритм решения задачи на вычисление доходности
1) определяются финансовые инструменты, доходность которых сравнивается между собой. При этом имеется в виду, что при нормально функционирующем рынке доходность различных финансовых инструментов приблизительно равна друг другу;
определяются типы финансовых инструментов, для которых требуется вычислить доходность;
выясняются известные и неизвестные переменные в формуле (11);
если в результате получилось выражение, позволяющее составить уравнение и решить его относительно искомого неизвестного, то уравнение решается и процедура решения задачи на этом заканчивается;
если не удалось составить уравнение относительно искомого неизвестного, то формулу (11), последовательно используя выражения (2) - (4), (6), (8), (9), приводят к такому виду, который позволяет вычислить неизвестную величину.
Рассмотрим несколько типовых вычислительных задач, решаемых с использованием предложенной методики.
Пример 1. Депозитный сертификат был куплен за 6 месяцев до срока его погашения по цене 10 000 руб. и продан за 2 месяца до срока погашения по цене 14 000 руб. Определите (по простой процентной ставке без учета налогов) доходность этой операции в пересчете на год.
Шаг 1. Тип ценной бумаги указан явно: депозитный сертификат. Эта ценная бумага, выпущенная банком, может принести своему владельцу как процентный, так и дисконтный доход.
Шаг 2.
d
=  .
.
Однако уравнения для решения задачи мы еще не получили, так как в условии задачи присутствует только Z – цена приобретения данного финансового инструмента, равная 10000 руб.
Шаг 3. Используем для решения задачи формулу (2), в которой Т = 12 месяцев и t = 6 – 2 = 4 месяца. Таким образом, = 3. В результате получаем выражение
d
=  .
.
Шаг 4. Из формулы (3), учитывая, что = 0, получаем выражение
d
=  .
.
Шаг 5. Используя формулу (4), учитывая, что Р пр = 14 000 руб. и Р пок = 10 000 руб., получаем выражение, которое позволяет решить поставленную задачу:
d =
(14 000 - 10 000) : 10 000 3 100 = 120%.
Рис. 10.2. Алгоритм решения задачи на сравнение доходностей
Пример 2.
Определите цену размещения Z
банком своих векселей (дисконтных) при условии, что вексель выписывается на сумму 200 000 руб. со сроком платежа t
2 = 300 дней, банковская процентная ставка равна (5) = 140% годовых. Год принять равным финансовому году (Т
1 = Т
2 = t
1 = 360 дней).
Шаг 1. Первый финансовый инструмент представляет собой депозитный вклад в банке. Второй финансовый инструмент является дисконтным векселем.
Шаг 2. В соответствии с формулой (10) доходность финансовых инструментов должна быть приблизительно равна друг другу:
d 1 = d 2 .
Однако эта формула не представляет собой уравнение относительно неизвестной величины.
Шаг 3. Детализируем уравнение, используя для решения задачи формулу (11). Примем во внимание, что Т 1 = Т 2 = 360 дней, t 1 = 360 дней и t 2 = 300 дней. Таким образом, 1 = l и 2 = 360: 300 = 1,2. Учтем также, что Z 1 = Z 2 = Z . В результате получаем выражение
 =
=  1,2.
1,2.
Данное уравнение также не может быть использовано для решения поставленной задачи.
Шаг 4. Из формулы (6) определяем сумму, которая будет получена в банке при выплате дохода по простой процентной ставке с одной; процентной выплатой:
D 1 = 1 = Z = Z l,4.
Из формулы (4) определяем доход, который получит владелец векселя:
D 2 = d 2 = (200 000 - Z ).
Подставляем данные выражения в формулу, полученную на предыдущем шаге, и получаем
Z =
=  l,2.
l,2.
Данное уравнение решаем относительно неизвестного Z
и в результате находим цену размещения векселя, которая будет равна Z
= 92 308 руб.
Частные методики решения вычислительных задач
Рассмотрим частные методики решения вычислительных задач, с которыми сталкиваются в процессе профессиональной работы на фондовом рынке. Рассмотрение начнем с разбора конкретных примеров.Собственные и заемные средства при совершении сделок с ценными бумагами
Пример 1. Инвестор решает приобрести акцию с предполагаемым ростом курсовой стоимости 42% за полугодие. Инвестор имеет возможность оплатить за счет собственных средств 58% от фактической стоимости акции (Z ). Под какой максимальный полугодовой процент () должен взять инвестор ссуду в банке, с тем чтобы обеспечить доходность на вложенные собственные средства на уровне не менее 28% за полугодие? При расчете необходимо учесть налогообложение прибыли (по ставке 30%) и тот факт, что проценты по банковской ссуде будут погашаться из прибыли до ее налогообложения.Решение. Рассмотрим сначала решение этой задачи традиционным пошаговым методом.
Шаг 1. Тип ценной бумаги (акция) задан.
Шаг 2. Из формулы (1) получаем выражение
d
=  100 = 28%,
100 = 28%,
где Z - рыночная стоимость финансового инструмента.
Однако решить уравнение мы не можем, так как из условия задачи известны только d - доходность финансового инструмента на вложенные собственные средства и доля собственных средств в приобретении данного финансового инструмента.
Шаг 3. Использование формулы (2), в которой T = t = 0,5 года, позволяет вычислить = 1. В результате получаем выражение
d
= 100 = 28%.
Данное уравнение также не может быть использовано для решения поставленной задачи.
Шаг 4. Принимая во внимание, что инвестор получает только дисконтный доход, формулу для дохода с учетом налогообложения (9) преобразуем к виду
D = d (1 - д) = d 0,7.
Отсюда выражение для доходности представляем в форме
d
=  = 28%.
= 28%.
Данное выражение также не позволяет решить поставленную задачу.
Шаг 5. Из условия задачи следует, что:
через полгода рыночная стоимость финансового инструмента возрастет на 42%, т.е. будет справедливо выражение Р пр = 1,42 Z ;
затраты на приобретение акции равны ее стоимости и выплаченным процентам по банковской ссуде, т.е.
Полученные выше выражения позволяют преобразовать формулу для дисконтного дохода (4) к виду
d = (Р пр - Р пок) = 42 Z (1 - ).
Используем данное выражение в полученной выше формуле для расчета доходности. В результате этой подстановки получаем
d
=  = 28%.
= 28%.
Данное выражение представляет собой уравнение относительно . Решение полученного уравнения позволяет получить ответ: = 44,76%.
Из приведенного выше видно, что данная задача может быть решена по формуле для решения задач, возникающих при использовании собственных и заемных средств при совершении сделок с ценными бумагами:
d =
 (13)
(13)
где d - доходность финансового инструмента;
К - рост курсовой стоимости;
- банковская ставка;
- доля заемных средств;
1 - коэффициент, учитывающий налогообложение дохода.
Причем решение задачи типа той, которая была приведена выше, будет сводиться к заполнению таблицы, определению неизвестного, относительно которого решается задача, подстановке известных величин в общее уравнение и решению полученного уравнения. Продемонстрируем это на примере.
Пример 2. Инвестор решает приобрести акцию с предполагаемым ростом курсовой стоимости 15% за квартал. Инвестор имеет возможность оплатить за счет собственных средств 74% от фактической стоимости акции. Под какой максимальный квартальный процент должен взять инвестор ссуду в банке, с тем чтобы обеспечить доходность на вложенные собственные средства на уровне не менее 3% за квартал? Налогообложение не учитывать.
Решение. Заполним таблицу:
| d | К | | | 1 |
| 0,03 | 0,15 | ? | 1 – 0,74 = 0,24 | 1 |
Общее уравнение приобретает вид
0,03 = (0,15 - 0,26) : 0,74 ,
который можно преобразовать в форму, удобную для решения:
= (0,15 – 0,03 . 0,74) : 0,26 = 0,26 ,
или в процентах = 26%.
Бескупонные облигации
Пример 1. Бескупонная облигация была приобретена на вторичном рынке по цене 87% к номиналу через 66 дней после своего первичного размещения на аукционе. Для участников этой сделки доходность к аукциону равна доходности к погашению. Определите цену, по которой облигация была куплена на аукционе, если срок ее обращения равен 92 дням. Налогообложение не учитывать.Решение. Обозначим - цену облигации на аукционе в процентах к номиналу N. Тогда доходность к аукциону будет равна
d
a = 
 .
.
Доходность к погашению равна
d
п = 
 .
.
Приравниваем d a и d п и решаем полученное уравнение относительно ( = 0,631, или 63,1%).
Выражение, которое использовалось для решения задач, возникающих при совершении сделок с бескупонными облигациями, можно представить в виде формулы
 = K
= K

 ,
,
где k - отношение доходности к аукциону к доходности к погашению;
- стоимость ГКО на вторичном рынке (в долях от номинала);
- стоимость ГКО на аукционе (в долях от номинала);
t - время, прошедшее после аукциона;
Т - срок обращения облигации.
В качестве примера рассмотрим следующую задачу.
Пример 2. Бескупонная облигация была приобретена в порядке первичного размещения (на аукционе) по цене 79,96% от номинальной стоимости. Срок обращения облигации - 91 день. Укажите, по какой цене должна быть продана облигация спустя 30 дней после аукциона, с тем чтобы доходность к аукциону оказалась равной доходности к погашению. Налогообложение не учитывать.
Решение. Представим условие задачи в виде таблицы:
| | | Т | t | k |
| ? | 0,7996 | 91 | 30 | 1 |
Подставляя данные таблицы в базовое уравнение, получаем выражение
( - 0,7996) : (0,7996 30) – (1 - ) : ( 61).
Его можно привести к квадратному уравнению вида
2 – 0,406354 - 0,3932459 = 0.
Решая данное квадратное уравнение, получаем = 86,23%.
Метод дисконтирования денежных потоков
Общие понятия и терминология
Если при сравнении доходностей в качестве альтернативной выбирается доходность депозитного вклада в банке, то изложенный общий метод альтернативной доходности совпадает с методом дисконтирования денежных потоков, который до последнего времени широко использовался в финансовых вычислениях. При этом возникают следующие основные вопросы:
величина ставки депозита коммерческого банка, принятая в качестве базовой;
схема начисления денег в банке (простого или сложного процента).
На второй вопрос ответить проще: рассматривают оба случая, т.е. начисления процентного дохода по простой и по сложной процентной ставке. Однако, как правило, предпочтение отдают схеме начисления процентного дохода по сложной процентной ставке. Напомним, что в случае начисления денежных средств по схеме простого процентного дохода он начисляется на основную денежную сумму, положенную на депозитный вклад в банке. При начислении денежных средств по схеме сложного процента доход начисляется как на исходную сумму, так и на уже начисленный процентный доход. Во втором случае предполагается, что инвестор не изымает сумму основного вклада и проценты по нему со счета в банке. В результате эта операция получается более рискованной. Однако она приносит и больший доход, что является дополнительной платой за больший риск.
Для метода численной оценки параметров операций с ценными бумагами на основе дисконтирования денежных потоков введен свой понятийный аппарат и своя терминология. Ее мы сейчас кратко изложим.
Приращение и дисконтирование. Различные варианты инвестиционных вложений имеют различные графики поступления платежей, что затрудняет их непосредственное сопоставление. Поэтому необходимо привести денежные поступления к одному моменту времени. Если этот момент находится в будущем, то такая процедура называется приращением, если в прошлом - дисконтированием.
Будущая стоимость денег. Деньги, имеющиеся у инвестора в настоящий момент времени, предоставляют ему возможность приумножить капитал путем их размещения на депозит в банке. В результате в будущем у инвестора будет большая сумма денег, которая называется будущей стоимостью денег. В случае начисления банковского процентного дохода по схеме простого процента будущая стоимость денег равна
P F = P C (1 + n )
Для схемы сложного процента это выражение принимает вид
P F = P C (1 + ) n
где Р F - будущая стоимость денег;
P C - первоначальная сумма денег (текущая стоимость денег);
- ставка банковского депозита;
п - число периодов начисления денежных доходов.
Коэффициенты (1+ ) n для сложной процентной ставки и (1 + n ) для простой процентной ставки называются коэффициентами наращения.
Первоначальная стоимость денег. В случае дисконтирования стоит обратная задача. Известна сумма денег, которую рассчитывают получить в будущем, и надо определить, сколько денег необходимо инвестировать в настоящее время, чтобы иметь заданную сумму в будущем, т.е., другими словами, необходимо вычислить
P
C =  ,
,
где сомножитель  -
называется коэффициентом дисконтирования.
Очевидно, что это выражение справедливо для случая начисления депозита по схеме сложного процентного дохода.
-
называется коэффициентом дисконтирования.
Очевидно, что это выражение справедливо для случая начисления депозита по схеме сложного процентного дохода.
Внутренняя ставка доходности. Эта ставка представляет собой результат решения задачи, в которой известны текущая стоимость вложений и их будущая стоимость, а неизвестной величиной является депозитная ставка банковского процентного дохода, при которой определенные инвестиции в настоящем обеспечат заданную стоимость в будущем. Внутренняя ставка доходности вычисляется по формуле
=  -1.
-1.
Дисконтирование денежных потоков. Денежные потоки - это доводы, полученные в разное время инвесторами от инвестиций в денежной форме. Дисконтирование, представляющее собой приведение будущей стоимости инвестиций к их текущей стоимости, позволяет сравнить различные виды инвестиций, сделанные в разное время и на разных условиях.
Рассмотрим случай, когда какой-либо финансовый инструмент приносит в начальный момент времени доход, равный С 0 , за период первых процентных выплат - С 1 , вторых - С 2 , …, за период n -х процентных выплат - С n . Суммарный доход от этой операции будет
D = C 0 + C 1 + C 2 +… + C n .
Дисконтирование данной схемы денежных поступлений к начальному моменту времени даст следующее выражение для вычисления значения текущей рыночной стоимости финансового инструмента:
C
0 +  +
+ +…+
+…+ = P
C . (15)
= P
C . (15)
Аннуитеты. В том случае, когда все платежи равны между собой, приведенная выше формула упрощается и приобретает вид
C
(1 +  +
+ +…+) =
+…+) =  P
C .
P
C .
В том случае, если эти регулярные платежи поступают ежегодно, они называются аннуитеты. Величина аннуитета вычисляется как
C
= .
.
В настоящее время этот термин часто применяется ко всем одинаковым регулярным платежам независимо от их периодичности.
Примеры использования метода дисконтирования денежных потоков
Рассмотрим примеры задач, для решения которых целесообразно использовать метод дисконтирования денежных потоков.Пример 1. Инвестору необходимо определить рыночную стоимость облигации, по которой в начальный момент времени и за каждый квартальный купонный период выплачивается процентный доход С в размере 10% от номинальной стоимости облигации N, а через два года по окончании срока обращения облигации - процентный доход и номинальная стоимость облигации, равная 1000 руб.
В качестве альтернативной схемы инвестиционных вложений предлагается банковский депозит на два года с начислением процентного дохода по схеме сложных процентных ежеквартальных выплат по ставке 40% годовых.
Решение. Для решения данной задачи используется формула (15),
где п = 8 (за два года будет осуществлено 8 квартальных купонных выплат);
= 10% (годовая процентная ставка, равная 40%, пересчитанная на квартал);
N = 1000 руб. (номинальная стоимость облигации);
С 0 – C 1 = С 2 - … = С 7 = С = 0,1N – 100 руб.,
C 8 = C + N = 1100руб.
Из формулы (15), используя условия данной задачи, для вычисления
C
(1+++…+)+=(N+C ).
).
Подставляя в данную формулу числовые значения параметров, получаем текущее значение рыночной стоимости облигации, равное P C = 1100 руб.
Пример 2. Определите цену размещения коммерческим банком своих дисконтных векселей при условии, что вексель выписывается на сумму 1 200 000 руб. со сроком платежа 90 дней, банковская ставка - 60% годовых. Банк начисляет процентный доход ежемесячно по схеме сложного процента. Год считать равным 360 календарным дням.
Сначала решим поставленную задачу, используя общий подход (метод альтернативной доходности), который был рассмотрен ранее. Затем решим задачу методом дисконтирования денежных потоков.
Решение задачи общим методом (методом альтернативной доходности). При решении поставленной задачи необходимо учесть основной принцип, который выполняется при нормально функционирующем фондовом рынке. Этот принцип состоит в том, что на таком рынке доходность различных финансовых инструментов должна быть приблизительно одинаковой.
Инвестор в начальный момент времени имеет некоторую сумму денег X, на которую он может:
либо купить вексель и через 90 дней получить 1200000 руб.;
либо положить деньги в банк и через 90 дней получить такую же сумму.
В первом случае (покупка векселя) доход равен: D = (1200000 – X ), затраты Z = X. Поэтому доходность за 90 дней равна
d 1 = D/Z= (1200000 – Х )/Х.
Во втором случае (размещение денежных средств на банковский депозит)
D = X (1 + ) 3 – X , Z = X .
d 2 - D/Z= [X (1+) 3 - Х /Х.
Отметим, что в данной формуле используется - банковская ставка, пересчитанная на 30 дней, которая равна
- 60 (30/360) = 5%.
d 1 = d 2), получаем уравнение для вычисления X:
(1200000 - Х )/Х- (X 1,57625 - Х )/Х.
X, получим X = 1 036 605,12 руб.
Решение задачи методом дисконтирования денежных потоков. Для решения данной задачи используем формулу (15). В этой формуле сделаем следующие подстановки:
процентный доход в банке начислялся в течение трех месяцев, т.е. п = 3;
банковская ставка, пересчитанная на 30 дней, равна - 60 (30/360) - 5%;
на дисконтный вексель промежуточные выплаты не производятся, т.е. С 0 = С 1 = С 2 = 0;
по истечении трех месяцев происходит гашение векселя и по нему выплачивается вексельная сумма, равная 1 200 000 руб., т.е. С 3 = 1200000руб.
Подставляя приведенные числовые значения в формулу (15), получаем уравнение Р с = 1 200 000/(1,05) 3 , решив которое, получим
P C = 1 200 000: 1,157625 - 1 036 605,12 руб.
Как видно, для задач данного класса методы решения эквивалентны.
Пример 3. Эмитент выпускает облигационный заем на сумму 500 млн руб. сроком на один год. Купон (120% годовых) выплачивается при погашении. Одновременно эмитент начинает формировать фонд для погашения данного выпуска и причитающихся процентов, откладывая в начале каждого квартала некоторую постоянную сумму денег на специальный счет в банке, по которому банк производит ежеквартальное начисление процентов по сложной ставке 15% за квартал. Определите (без учета налогообложения) размер одного ежеквартального взноса, считая, что момент последнего взноса соответствует моменту погашения займа и выплаты процентов.
Решение. Эту задачу удобнее решать методом приращения денежного потока. Через год эмитент обязан возвратить инвесторам
500 + 500 1,2 = 500 + 600 = 1 100 млн руб.
Эту сумму он должен получить в банке в конце года. При этом инвестор осуществляет следующие вложения в банк:
1) в начале года X руб. на год под 15% ежеквартальных выплат в банке по ставке сложного процента. С этой суммы у него в конце года будет Х (1,15) 4 руб.;
2) по истечении I квартала X руб. на три квартала на тех же условиях. В результате в конце года с этой суммы у него будет Х(1,15) 3 руб.;
3) аналогично вложение на полгода даст в конце года сумму Х(1,15) 2 руб.;
4) предпоследнее вложение на квартал даст к концу года Х(1,15)руб.;
5) и последний взнос в банке в размере X совпадает по условию задачи с погашением займа.
Таким образом, осуществив денежные вложения в банк по указанной схеме, инвестор в конце года получит следующую сумму:
Х (1,15) 4 + Х (1,15) 3 + Х (1,15) 2 + Х (1,15) +X = 1100 млн руб.
Решая данное уравнение относительно X, получаем Х = 163,147 млн руб.
Примеры решения некоторых задач
Приведем примеры решения некоторых задач, которые стали классическими и используются при изучении курса «Рынок ценных бумаг».Рыночная стоимость финансовых инструментов
Задача 1. Определите цену размещения коммерческим банком своих векселей (дисконтных) при условии: вексель выписывается на сумму 1 000 000 руб. со сроком платежа 30 дней, банковская ставка - 60% годовых. Считать год равным 360 календарным дням.
Решение. При решении поставленной задачи необходимо учесть основной принцип, который выполняется при нормально функционирующем фондовом рынке. Этот принцип состоит в том, что на таком рынке доходность различных финансовых инструментов должна быть приблизительно одинаковой. Инвестор в начальный момент времени имеет некоторую сумму денег X, на которую он может:
либо купить вексель и через 30 дней получить 1 000 000 руб.;
либо положить деньги в банк и через 30 дней получить такую же сумму.
Поэтому доходность за 30 дней равна
d 1 = D/Z - (1 000 000 - Х )/Х.
Во втором случае (банковский депозит) аналогичные величины равны
D - X(1+) - X; Z = X; d 2 = D/Z= [Х(1+) - Х ]/Х.
Отметим, что в данной формуле используется - банковская ставка, пересчитанная на 30 дней и равная: = 60 30/360 = 5%.
Приравнивая друг другу доходности двух финансовых инструментов (d 1 = d 2), получаем уравнение для вычисления X:
(1 000 000 - Х )/Х - (X 1 ,05 - Х )/Х.
Решая это уравнение относительно X, получим
Х= 952 380,95 руб.
Задача 2. Инвестор А купил акции по цене 20 250 руб., а через три дня с прибылью продал их инвестору В, который в свою очередь, спустя три дня после покупки, с прибылью перепродал эти акции инвестору С по цене 59 900 руб. По какой цене инвестор В купил указанные бумаги у инвестора А, если известно, что оба этих инвестора обеспечили себе одинаковую доходность от перепродажи акций?
Решение. Введем обозначения:
P 1 - стоимость акций при первой сделке;
Р 2 - стоимость акций при второй сделке;
Р 3 - стоимость акций при третьей сделке.
Доходность операции, которую смог обеспечить себе инвестор А:
d a = (P 2 – P 1)/P 1
Аналогичная величина для операции, выполненной инвестором В:
d B = (Р 3 - Р 2)/Р 2 .
По условию задачи d a = d B , или P 2 /P 1 - 1 = Р 3 /Р 2 - 1.
Отсюда получаем Р 2 2 = Р 1 , Р 3 = 20250 - 59900.
Ответ данной задачи: Р 2 = 34 828 руб.
Доходность финансовых инструментов
Задача 3. Номинальная стоимость акций АО - 100 руб. за акцию, текущая рыночная цена - 600 руб. за акцию. Компания выплачивает квартальный дивиденд в размере 20 руб. на акцию. Чему равна текущая доходность акций АО в годовом исчислении?
Решение.
N = 100 руб. - номинальная стоимость акции;
X = 600 руб. - рыночная цена акции;
d K = 20 руб/квартал - доходность облигации за квартал.
Текущая доходность в годовом исчислении d г определяется как частное от деления дохода за год D на затраты на приобретение данного финансового инструмента X:
d г = D/X.
Доход за год вычисляется как суммарный поквартальный доход за год: D = 4 d г - 4 20 = 80 руб.
Затраты на приобретение определяются рыночной ценой данного финансового инструмента Х=600 руб. Текущая доходность равна
d г = D/X = 80: 600 = 0, 1333, или 13,33%.
Задача 4. Текущая доходность привилегированной акции, объявленный дивиденд которой при выпуске 11%, а номинальная стоимость 1000 руб., в текущем году составила 8%. Корректна ли такая ситуация?
Решение. Обозначения, принятые в задаче: N = 1000 руб. - номинальная стоимость акции;
q = 11% - объявленный дивиденд привилегированной акции;
d г = 8% - текущая доходность; X = рыночная цена акции (неизвестна).
Приведенные в условии задачи величины связаны между собой соотношением
d г = qN/X.
Можно определить рыночную цену привилегированной акции:
X - qN/d г - 0,1 1 1000: 0,08 - 1375 руб.
Таким образом, описанная в условиях задачи ситуация корректна при условии, что рыночная цена привилегированной акции составляет 1375 руб.
Задача 5. Как изменится в процентах к предыдущему дню доходность к аукциону бескупонной облигации со сроком обращения один год (360 дней), если курс облигации на третий день после проведения аукциона не изменится по сравнению с предыдущим днем?
Решение.
Доходность облигации к аукциону (в пересчете на год) на третий день после его проведения определяется по формуле
d
3 = 
 .
.
где X - аукционная цена облигации, % к номиналу;
Р - рыночная цена облигации на третий день после аукциона.
Аналогичная величина, рассчитанная на второй день, равна
d
2 = .
.
Изменение в процентах к предыдущему дню доходности облигации к аукциону:
 = -= 0,333333,
= -= 0,333333,
или 33,3333%.
Доходность облигации к аукциону уменьшится на 33,3333%.
Задача 6. Облигация, выпущенная сроком на три года, с купоном 80% годовых, продается с дисконтом 15%. Вычислить ее доходность до погашения без учета налогообложения.
Решение. Доходность облигации до погашения без учета налогообложения равна
d
= ,
,
где D - доход, полученный по облигации за три года;
Z - затраты на приобретение облигации;
- коэффициент, пересчитывающий доходность на год.
Доход за три года обращения облигации состоит из трех купонных выплат и дисконтного дохода при погашении. Таким образом, он равен
D = 0,8N 3 + 0,15 N = 2,55 N .
Затраты на приобретение облигации равны
Z = 0,85N.
Коэффициент пересчета доходности на год, очевидно, равен = 1/3. Следовательно,
d
= = 1, или 100%.
= 1, или 100%.
Задача 7. Курс акций вырос за год на 15%, дивиденд выплачивался раз в квартал в размере 2500 руб. за акцию. Определите полную доходность акции за год, если в конце года курс составил 11500 руб. (налогообложение не учитывать).
Решение. Доходность акции за год вычисляется по формуле
d = D/Z,
где D - доход, полученный владельцем акции;
Z - затраты на ее приобретение.
D - вычисляется по формуле D = + ,
где - дисконтная часть дохода;
- процентная часть дохода.
При этом = (Р 1 - P 0 ),
где Р 1 - цена акций к концу года;
P 0 - цена акций в начале года (отметим, что P 0 = Z).
Так как в конце года стоимость акции была равна 11 500 руб., причем рост курсовой стоимости акций составил 15%, то, следовательно, в начале года акция стоила 10 000 руб. Отсюда получаем:
= 1500руб.,
= 2500 4 = 10 000 руб. (четыре выплаты за четыре квартала),
D = + = 1500 + 10 000 = 11 500 руб.;
Z = P 0 = 10000руб.;
d = D/Z= 11500: 10000 = 1,15, или d = 115%.
Задача 8. Векселя со сроком платежа, наступающим через 6 месяцев от составления, реализуются с дисконтом по единой цене в течение двух недель от момента составления. Считая, что каждый месяц содержит ровно 4 недели, рассчитайте (в процентах) отношение годовой доходности по векселям, купленным в первый день их размещения, к годовой доходности по векселям, купленным в последний день их размещения.
Решение. Годовая доходность по векселям, купленным в первый день их размещения, равна
d 1 = (D/Z ) - 12/t = /(1 - ) 12/6 = /(1 - ) . 2,
где D - доход по облигации, равный D = N;
N - номинал облигации;
- дисконт в процентах от номинала;
Z - стоимость облигации при размещении, равная Z = (1 - ) N;
t - время обращения облигации, купленной в первый день ее выпуска (6 месяцев).
Годовая доходность по векселям, купленным в последний день их размещения (через две недели), равна
d 2 = (D/Z ) 12/ t = /(1 - ) - (12: 5,5) = /(1 - ) . 2, 181818,
где t - время обращения облигации, купленной в последний день ее выпуска (через две недели), равное 5,5 месяца.
Отсюда d 1 /d 2 = 2: 2,181818 = 0,9167, или 91,67%.
Оценку денежных потоков и их приведение к одному моменту времени можно производить на номинальной или на реальной основе.
Номинальные денежные потоки и поминальные ставки. Номинальные денежные потоки - это денежные суммы, выраженные в ценах, изменяющихся в связи с инфляцией, т.е. платежи, которые действительно будут уплачены или получены в различные будущие моменты (интервалы) времени. При их расчете учитывается постоянный рост уровня цен в экономике, и это оказывает влияние на денежную оценку затрат и результатов принятия инвестиционного решения (рис. 3.3).
Например, решив осуществить проект открытия мини-пекарни для выпечки и продажи хлебобулочных изделий, мы должны в расчетах ожидаемых денежных потоков учесть прогнозируемый рост цеп на хлеб, муку и т.п. в течение срока жизни проекта и соответствующим образом проиндексировать денежные потоки на повышающий коэффициент.
Рис. 3.3.
Номинальная ставка альтернативной (требуемой) доходности - это ставка, действительно существующая на рынке для инвестиционных решений данного уровня риска. В период высокой инфляции такие ставки возрастают, чтобы за счет повышенных доходов компенсировать инвесторам потери от инфляционного роста цен. Наоборот, номинальные ставки относительно низки в период стабилизации цен. Основываясь на этом, говорят, что данные ставки включают в себя инфляционную премию.
Реальные денежные потоки и реальные ставки дисконта. Реальные денежные потоки - это потоки, выраженные в постоянном масштабе цен, действующем на момент обоснования инвестиционного решения. Таким образом, они оцениваются без учета инфляционного роста цен (рис. 3.4). Однако денежные потоки все равно должны быть проиндексированы на понижающий или повышающий коэффициент, если они (или отдельные их элементы) растут быстрее или медленнее инфляции.

Рис. 3.4.
Реальная ставка альтернативной (требуемой) доходности- это ставка, "очищенная" от инфляционной премии. Она отражает часть доходов инвестора, образующуюся сверх компенсации инфляционного роста цен.
Реальная ставка (г) рассчитывается по формуле
![]()
где гр - реальная ставка; г - номинальная ставка; к - темп инфляции. Все ставки выражаются в долях единицы.
Пример . Ставка банковского процента по вкладам равна 6%, а инфляция в этот период ожидается на уровне 10%. Какова реальная ставка доходности, предлагаемая банком?

Реальные денежные потоки дисконтируются по реальным ставкам, номинальные - по номинальным.
Базовое правило расчетов состоит в том, что:
- o реальные денежные потоки следует дисконтировать по реальным ставкам альтернативной доходности;
- o номинальные денежные потоки следует дисконтировать, используя номинальные ставки дисконта.
Таким образом, существуют два подхода к оценке денежных потоков, каждый из которых имеет свои плюсы и минусы.
Преимущества и недостатки метода оценки в постоянных (фиксированных) ценах. Преимуществом оценки на реальной основе является то, что при укрупненном расчете денежных потоков нет необходимости прогнозировать будущий инфляционный рост цен - достаточно знать текущий уровень инфляции и действующие в текущем периоде цены. Вместе с тем для осуществления такого расчета необходимо более или менее строгое выполнение следующей гипотезы: все цены на продукцию, сырье, материалы и т.п., принятые при определении денежных потоков, изменяются в одной пропорции в соответствии с уровнем инфляции в экономике. Еще один "минус" - при таком подходе возникают трудности анализа систем финансирования проектов (к реальным ставкам необходимо приводить и процентные ставки по кредитам, предоставленным для осуществления инвестиционного решения, что порождает недоверие к результатам расчета со стороны кредиторов). Например, они дают деньги под 14% годовых, а в расчетах фигурирует реальная ставка - 4%. К тому же бюджет проекта, составленный на номинальной основе, смотрится более реалистично.
Рассмотрим принципиальный подход к оценке на реальной и номинальной основе на примере.
Пример . Менеджер компании предполагает, что проект потребует инвестиций в размере 350 млн руб. и в первый год осуществления даст денежный поток 100 млн руб. В каждый последующий год в течение пяти лет денежный поток будет возрастать на 10% в связи с инфляционным ростом цен на продукцию и затраты. На шестой, завершающий год, от продажи оборудования будет получен суммарный денежный поток в размере 123 млн руб. Необходимо определить, выгоден ли данный проект, если номинальная ставка альтернативной доходности равна 20% годовых.
Денежный поток по проекту с учетом инфляционного роста показан в табл. 3.6.
ТАБЛИЦА 3.6.
Чистый дисконтированный доход рассчитывается следующим образом:
ЫРУ> О, значит, проект выгоден.
Произведем оценку того же проекта на реальной основе. Реальная ставка альтернативной доходности вычисляется по формуле
По условию, ожидается только инфляционный рост цен. Поэтому последующий денежный поток вплоть до шестого года будет стабилен и равен 100: 1,1 = 90,91 млн руб. Денежный поток последнего года, рассчитанный в постоянном масштабе цен, равен

Как видно, оба метода дали практически одинаковый результат, что объясняется одинаковыми предположениями, заложенными в условиях примера для обоих подходов (расхождения связаны с погрешностью приближения, допущенной в расчетах).